一、游戏数学
1.基于SDF的摇杆移动
SDF:
SDF全称Signed Distance Field(有号距离场),定义为空间中的点到形状表面的最小距离,并用正值表示点在形状外部,负值表示点在形状内部。
为什么要使用SDF?
空间换时间,在O(1)时间复杂度计算出是否碰撞。
如何判断碰撞?
基于已有SDF信息的栅格,使用其邻近四个角的SD信息进行插值,得到当前点的SD,若SD<=0, 则判定该点和碰撞物发生了碰撞。
插值获得任意点的SD值:
1 | |
如何实现发生碰撞后绕障碍物滑行?
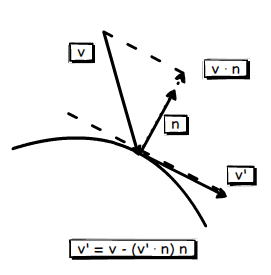
v表示摇杆方向,与障碍物发生碰撞后需要沿着v’方向滑行,n为碰撞法线,v’和v有以上关系。
如何获取碰撞法线n?
利用SDF的梯度作为碰撞法线。
求梯度方向:
1 | |
发生碰撞后实际移动方向代码:
1 | |
角色不能越过障碍物的远距离移动
用于当校色进行瞬时远距离移动但不能越过障碍物的情况。
使用连续碰撞检测规避穿越障碍物的情况,具体方法是圆盘投射(Disk Casting)。
使用圆盘投射计算位置:
1 | |
动态地图
在均匀网格地图上,当角色在一帧内的行走距离不会超过单个网格大小时,可以通过检测每一帧与玩家所在网格相邻的8个网格的碰撞来实现规避障碍物的功能。
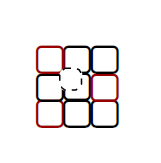
红色为障碍物区域,虚线圆圈为角色。
实现规避障碍物:
1 | |
场景中的其他障碍物,如较大的汽车、其他玩家等,可通过矩形、圆形的SDF函数来表示,并将结果与网格地图取出的SDF做交集操作。
圆盘SDF:
1 | |
矩形SDF:
d = (x - c)R(-θ) - b
Φx = min(max(dx, dy), 0) + ||max(d, 0)||
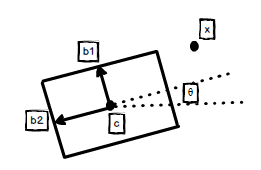
1 | |
2. 高性能的定点数实现方案
用途
解决不同平台上的浮点数运算结果不同而导致的对帧同步的严重影响。
32位浮点数结构
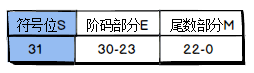
S=0时为正数,S=1时为负数
基于整数的二进制表示的定点数原理
设a为定点数,f(a)为这个定点数对应的整数值
a = 2^-n^f(a)
32和64位定点数表示原理
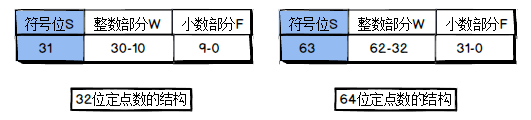
32位定点数表示的范围:[-2^21^, 2^21^ - 2^-10^]
64位定点数表示的范围:[-2^31^, 2^31^ - 2^-32^]
定点数四则运算
a + b = 2^-n^ (f(a) + f(b))
a - b = 2^-n^ (f(a) - f(b))
ab = (2^-n^)^2^ f(a) f(b) = 2^-n^ (2^-n^ f(a) f(b))
a / b = 2^-n^ (2^n^ f(a) / f(b))
二、游戏物理
1. 一种高效的弧长参数化路径系统
需求
在跑酷游戏中,人物的移动靠路径引导;想要实现“弧长参数化”的特性—即令曲线参数t与曲线长度为L为线性关系,从而将参数t的线性变化映射到长度的线性变化上,实现曲线上的匀线速度运动。
曲线路径系统需求:
路径布置简单,最直观的就是布置路点。
修改具有局部性,修改一个路点只会影响上下游。
曲线至少具有C1连续性,满足基本的光滑需求。
两个路点之间的曲线可以是异面曲线,等同于可以自由控制邻接路点曲线的方向。
与曲线相关的计算尽量简单,尽量少地进行迭代计算。
端点间二次样条的构建
为什么要拼接两条二次曲线?
要求两个路点可以自由控制位置和朝向(切线方向),单一的一段二次曲线自由度不够。
二次样条曲线:
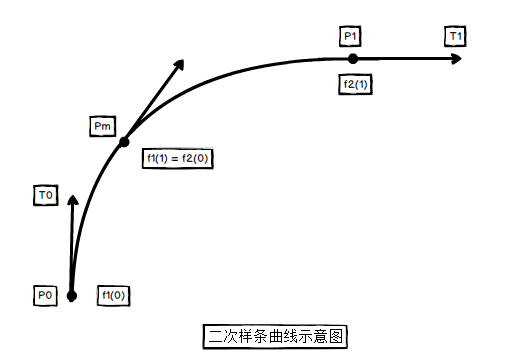
起点P0、起点切线T0、终点P1、终点切线T1。
f1(t) = a1t^2^ + b1t + c1
f2(t) = a2t^2^ + b2t + c2
为了将分段曲线当作一段曲线使用,需将两段曲线的参数t归一化到统一的[0, 1]范围内,fs(0) = P0,fs(1) = P1。

例如当L1长度为4,L2长度为6,归一化t = 0.3时,fs(t) = fs(0.3) = f1(0.3 x 10 / 4) = f1(3/4),恰好对应L1的四分之三位置。
路径的构建
路径为路点间曲线的拼接,切线的设置模仿Catmull-Rom这类Cardinal曲线的做法:路点i处的切线由路点i-1和路点i+1的位置决定:
Ti = τ(Pi+1 - Pi-1), τ为切线的缩放因子(张弛因子)
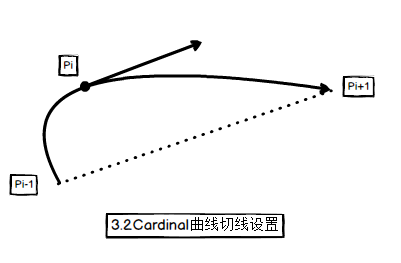
使用邻接路点的信息构建曲线时,将邻接路点转换到自己的局部坐标系下,在上图的构建中,Pi处于坐标原点且旋转为(0, 0, 0),最后在使用路径时,每段曲线的计算结果要做一次从局部到世界坐标系的转换,好处是路径作为一个整体不受刚体变换的影响,适合游戏中场景动态拼接的需求。
弧长的重参数化(arc-length parametrization)
为什么要做弧长的重参数化?
可近似理解为在曲线上,每一点处的速度不同,相同的Δt内对应“走过”的弧长也不相同。
例如,对于曲线:
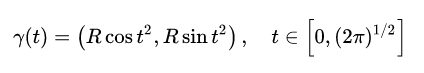
直接用t取点,具有明显不均匀现象:
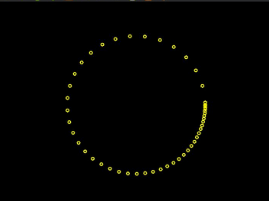
arc-length:
定义一个映射Δ: [a, b] -> [0, L], 获取原弧线参数t的定义域到弧长区间上的一个满射:
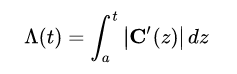
其反函数设为Φ(s),那么在给定s位置下,对应曲线参数为Φ(s),对于上述曲线,先求Δ(t),再求其反函数:
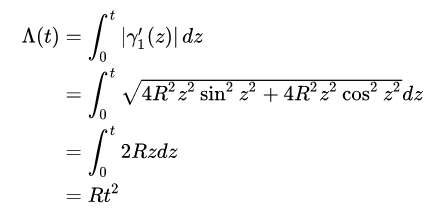
其反函数:
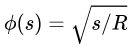
重参数化形式:
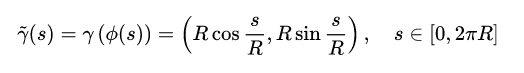
arc-length参数化后结果:

曲线上的简单运动
法平面定义:过空间曲线的切点并且与切线垂直的平面。
相邻路径的切换
路径切换的过程中,使用当前路径上的基准点的法平面与另一路径的交点(等位点),由于路径的切换不能瞬时完成,将当前基准点变换到相邻路径基准点的局部坐标系下,将变换后的值和(O, X, Y, Z)插值的结果转换到世界坐标系,作为当前基准点及其关联的局部坐标系输入给物理模块。
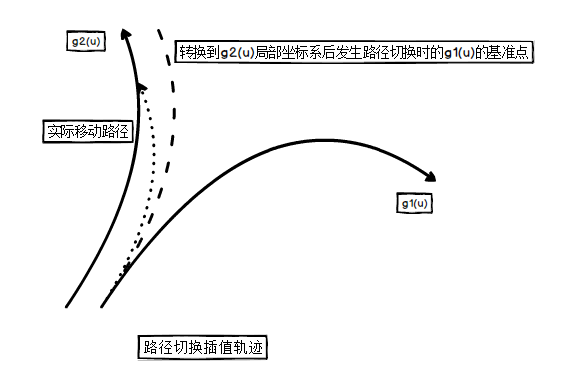
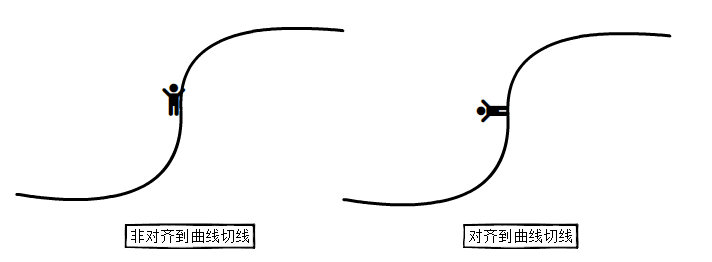
曲线上的旋转插值
2. 船的物理模拟及同步设计
船的两种刚体
移动碰撞体:用于计算浮力的动态刚体
射击碰撞体:用来做射击检测的动力学动态刚体
浮力计算中计算多面体入水体积
分成三角面判断,一个三角面只有三种状态:完全入水、完全出水、部分出水。
三角面完全入水,则三角面可以和P形成四面体为入水体积(点P必须在水面上)。
三角面完全出水,丢弃。
三角面部分入水,分两种情况,两点入水和一点入水。两点入水,分成的三个三角形,将水面上部的丢弃;一点入水,分成的三个三角形将水面上的两个三角形丢弃。
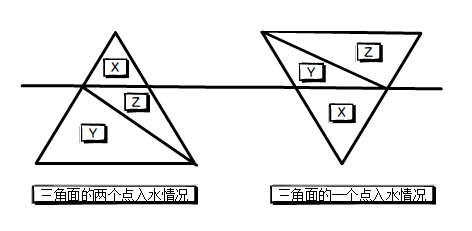
于是,入水体积的求解收敛为两个问题:
求一个四面体的体积。
已知三角形的顶点A, B, C, 求与水面的交点问题。
浮力系统物理更新机制
三种第三方位置同步方法:
设置位置:会造成物体瞬移。
设置速度:通过计算位移差求出速度,在物理引擎进行物理模拟前应用到动态刚体上。
设置力:增加了一层间接性。
问题:
第三方同步组件会每帧更新刚体的速度,浮力组件会每帧更新刚体受到的力,会造成位置的不一致(例如第三方刚体本来以速度v移动到位置X,但是浮力组件在速度方向上施加了阻力、浮力和升力,从而使物理系统算出的速度和v有偏差,导致最终物理模拟结束时物体的位置不是X)。
解决:
浮力系统根据是否是第一方选择最终计算结果是力还是速度。
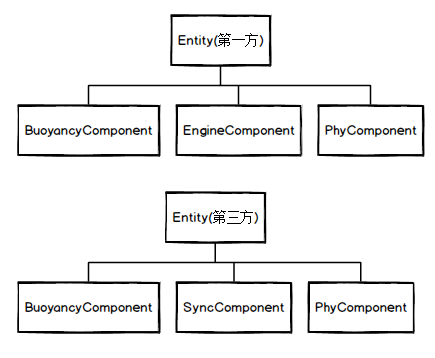
Component物理更新的过程:
第一方通过引擎组件(EngineComponent)计算出驱动力,通过浮力组件(BuoyancyComponent)计算出浮力,将这些力在物理引擎进行物理模拟之前统一施加在刚体组件(PhyComponent)上;
第三方通过同步组件(SyncComponent)计算出下一帧的同步速度,通过浮力组件计算出的浮力推算出下一帧的浮力速度,将这两个速度糅合后,在物理引擎进行物理模拟之前设置在刚体组件上。